Abdel Irada: <<•>A matter of degree<•>>We may already say that White is ahead on material. The apparent reply to the key move is 28. ...Rxf7?, however, this merely offers Black a way to lose a rook thanks to the consequent knight fork.
Is a pawn enough to claim a win? As it turns out, this too is irrelevant, for the key contains a threat that must be met, and White will emerge from the smoke and shocks of battle with another pawn in hand. *Two* pawns, as a rule, should be enough for a win.
So, how do we get there?
<<•>28. Rxe4...>
I withhold an exclam because this isn't a real queen sac. It does, however, create a nasty threat: 29. Rh4, when Black will be mated by Qxh7 if he doesn't take, and by Qxf8 if he does.
There appear to be two really relevant defenses, as well as many irrelevant ones.
<(1) 28. ...Qf6>
Now Black threatens to take on f7, so Rh4 is no longer playable, but White has better.
<29. Nxg6†, hxg6
30. Rh4†, Qxh4
31. Qxf8†, Kh7
32. Qxc8, Qxd4
33. Qxb7†, Kh6
34. g3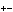 
>
White is two clear pawns up and the back-rank threat has been eliminated. Objectively, this should be enough. Note that this also applies if Black plays 28. ...Qe7, which transposes into the preceding line.
It can now be argued: The knight on c8 fell to a fork, so let's move it. But where will that lead?
<(2) 28. ...Nd6>
Here's what looks a formidable defense: The knight now forks queen and rook, so there's no time for a quiet move. Fortunately, White has loud ones.
<29. Nxg6†, hxg6
30. Rh4†, Qxh4
31. Qxf8†, Kh7
32. Qxd6 >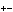
Again, White is two clear pawns to the good. But again, this appears to depend on the black knight's being on a vulnerable square.
Just for illustrative purposes: What happens, then, if Black puts it on a safe square?
<(3) 28. ...Na7?
29. Rh4, Qxh4>
As before, Black loses a rook with 29. ...Rxf7, although this is better than what follows.
<30. Qxf8#>
As we see, the knight can be "saved" only at the expense of the king or the rook. In other words, Black has no better defense than lines (1) and (2).
On the whole, this is a quite forthright problem with a tiny variation-tree. Its principal instructive value lies in its illustration of the principle of the illusory threat: Black doesn't really threaten ...Rxf7, and from that flows everything else we need.
Kibitzing
sac: 24.Qf4
(-0.45): 2.Ng4 Bxd4 3.Bg5 Rf8 4.Bxd8 Rxf7 5.Rxe4 Bxb2 6.Ba5 Kg7 7.Rxe6 Bxa3 8.Re8 Rd7 9.Kf1 Nd6 10.Bc3+ Kf7 11.Re3 Nc4 12.Rf3+ Ke6 13.Rf4 Nd6 14.Rf6+ Kd5 15.Rf3 Re7 16.Nf6+ Kc6 17.Rh3 b5
(-0.81): 2.Bf4 Nd6 3.Qd7 Rf8 4.Qxe6 Bg7 5.g3 Rf6 6.Qd7 Qxd7 7.Nxd7 Rxf4 8.gxf4 Bxd4 9.b4 Bd5 10.Kf1 Bc4+ 11.Kg1 Kg8 12.Rd1 Nf5 13.Rc1 Bd5 14.Ne5 Nd6 15.Rc7
(-2.58): 2.Rxe4 Nd6 3.Rf4 Bxe5 4.Qf8+ Rxf8 5.Rxf8+ Qxf8 6.Bxf8 Bf4 7.g3 Kg8 8.Bxd6 Bxd6 9.f4 Kf7 10.Kf2 Kf6 11.Kf3 Kf5 12.h3 h5 13.b4 Bf8 14.g4+ hxg4+ 15.hxg4+ Kf6 16.Ke4 g5 17.Ke3 gxf4+ 
