|
< Earlier Kibitzing · PAGE 22 OF 57 ·
Later Kibitzing> |
| Oct-14-09 | | amadeus: < (I have used top 100) > Working with the data from top players, professionals, is already problematic, I can only imagine how awful (and at the same time interesting) the full data is. But I think that would be too much for me. I hope you have the number of games. As for birthdate etc, you can probably use the first appearance as a parameter, in order to understand how the players develop; this should prove interesting -- I read somewhere that if you do not reach a good level (rating) after some time, you'll probably never get in there (I think it was in a chessbase article, but I'm not sure). |
|
| Oct-14-09 | | amadeus: Btw, concerning Carlsen's performance (3003) in Pearl Spring and Sonas' adjustment for inflation, of course the inflation problem is a serious one and everything, but I think Chessmetrics formula is a more important issue here -- because it's unecessary, and, in my opinion, not a good one. Adding 4 fake draws against the same average opposition, and 3 fake draws agains 2300, and then adding 43 points? I am sure this makes sense in his scheme of things, but I don't think it's a great way (or the best way) to calculate TPRs. The traditional ways are imo better, namely: (i) use elo rating (in case of infinity we have a problem, but adding a fake draw against youserlf is probably better than nothing - alexmagnus had some ideas concerning this issue, but I don't remember very well now) (ii) add or subtract 400 points (+op. rating) for win or a loss, take the average etc. In any way, I would like to add that, after analyzing a couple of past tournaments, 200~215/square root of n (n is the number of games) seems to be a good enough estimate for the uncertainty (standard deviation, I mean) of the performance. [for a very small number of games (1-3), it's probably a bit larger than that, small samples are always a problem... but I can live with that too: this is not rocket science, and none is going to die because of 5-10 points gone wrong] |
|
Oct-14-09
 | | alexmagnus: <amadeus> My idea for 100% was to subtract 0.25 points from the result. Actually doing it with <any> result, not just 100%, solves Sonas' main postulated problem - performance being (in)dependent of the number of games. With this method (-0.25 points) it becomes dependent, the more games the less role that subtraction plays :) I also explained why 0.25 - because then we get the lowest rating which is expected to score this level. |
|
| Oct-14-09 | | amadeus: <alexmagnus: My idea for 100% was to subtract 0.25 points from the result> That sounds good too. You put that together with the expected uncertainty, and we have a more meaningful result. I'm not sure about taking 0.25 from everyone though. If a player has a 0 score, e.g., I think we should add 0.25 points. But I'll keep that on mind. (Anyway, the major problems are 0% and 100% performances, and that will be taken care of) |
|
| Oct-14-09 | | Everyone: <amadeus> You'll be sorry if you do that. |
|
Oct-15-09
 | | alexmagnus: <amadeus> An improvement to my idea: add 0.25 points to results below 50% and subtract from those above 50%. The 50% results remain untouched. |
|
| Oct-15-09 | | amadeus: <alexmagnus>, I have thought about it, and I think (1/2 - %)*0.5 could be an improvement. For %=0 or 1, we still have 0.25; extreme performances are more affected by this adjust than those close to = (if equal, no adjust), but the main point is that e.g.: in Linares 2001 we had one player with a +5, and five players with a -1. If we take 0.25 from Kasparov, and add +0.25 to the others, we will end with 31 points for 30 games. If we use (1/2-%)*0.5, we add as much negative as positive points (zero sum), because the mean % is always 1/2 -- so we end with 30 points for 30 games, which I guess it's better. Pearl Spring would look like:
Carlsen: 7.85
Topalov: 5.48
Wang Yue: 4.52
Others: 4.05
If Nanjing were 5 games long (with the same final %), we would have: Carlsen: 3.85
Topalov: 2.73
Wang Yue: 2.27
Others: 2.05
Carlsen still loses the same amount of points in both cases, as in the original idea, but only 0.15. (5 games: 77%, 10 games: 78.5%, infinite games: 80%) PS: I had thought about 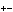 (1/2-%)^2 also, but the sum of the squares don't go to zero :/ (1/2-%)^2 also, but the sum of the squares don't go to zero :/ |
|
Oct-15-09
 | | alexmagnus: <amadeus> Hm. It makes perfect sense, at least at the first glance :). Probably you just found the ideal performance formula hehe. |
|
| Oct-18-09 | | Alexandru Z: <alexmagnus>, your idea of introducing these dominator lists is charming, and it might be worth considering it in other contexts too. I have some remarks about this, and will start posting them below. <amadeus>, thanks for including me in the list of recipients. I'll look into it as soon as time permits. |
|
| Oct-18-09 | | Alexandru Z: Let us consider the following general setting, unrelated to chess, players, or ratings. Suppose someone gives us n real numbers, not necessarily positive and not necessarily distinct, and tells us that he is not really interested in the numbers themselves, but in the differences between these numbers. More specifically, he wants to have a sense of how much the largest of the numbers dominates the others, and asks our opinion about it. Let's start by arranging the numbers in decreasing order, x_1, x_2,...,x_n say, and form what we refer to as <the list>, call it L.
L=(x_1,x_2,...,x_n).
Next, let's consider the differences between consecutive elements in the list: a_1=x_1-x_2, a_2=x_2-x_3, and so on. Thus the numbers a_1, a_2, ... , a_(n-1) are non-negative (that is, positive or zero). Let us now fix some weights: w_1, w_2, ..., w_(n-1). We require these weights to be non-negative real numbers, but other than that we choose them as we please, unlike the initial numbers x_1,... which are <given>. Let W denote this sequence of weights, W=(w_1,...,w_(n-1)). We refer to W as <the weight>. Next, multiply the differences a_1,... by the corresponding weights w_1,... and add them up. Denote the sum by D(W,L). D(W,L)=w_1a_1 + w_2a_2+...+w_(n-1)a_(n-1).
We interpret D(W,L) as a measure of how much x_1 dominates the rest of the list L <with respect to the weight W>. Example 1. Let W be given by: w_1=w_2=...=w_9=1, and let all the other weights (w_10, w_11 ,...) be equal to zero. Then: D(W,L) = a_1+a_2+...+a_9 = x_1-x_10. So this is the difference between #1 and #10 on the list, as considered by <alexmagnus> above. Example 2. Let W be given by w_1=...=w_99=1, and all the other weights equal to zero. Then this time D(W,L) measures the difference between #1 and #100 on the given list. Example 3. Let W be given by w_1=1, and all the other weights zero. In this case D(W,L) measures the gap between #1 and #2 on the given list, as I've done on that puzzle a few days ago on Carlsen's page, and applied it for each country individually. Before going any further, let me point to an example which does not refer to a rating list, but is still chess related. |
|
| Oct-18-09 | | Alexandru Z: Let us consider Carlsen's performance in rated tournaments in the last couple of years, and collect them in a list. The 3000+ performance at Nanjing stands out, and it does make sense for someone to raise the question of how much this performance dominates the other in the list. So this is an example of the type considered in my previous post. This example also shows that the weight W should not be set in stone. There was reasonable motivation for <alexmagnus> to consider the difference between #1 and #100, or #1 and #10, in that context. But in this context, those weights may not be the most appropriate. Thus in each context we might want to first decide which weight we feel is the most appropriate. At the level of generality from my previous post, I don't view any weight as being ``the best'', or better than another weight. I would like to end my remarks on this topic by discussing separately three different types of weights, which kind of look interesting: exponential decaying weights, power weights, and Cauchy-Danailov weights. |
|
| Oct-19-09 | | Alexandru Z: <Cauchy-Danailov weights>. Danailov has a clear idea in mind when arguing that Topalov deserves the chess Oscar more than Anand. He uses smaller weights on those categories which favor Anand (such as holding the world champion title), and higher weights on those categories which favor Topalov (such as ranking and rating). Thus, when he speaks about the Anand-Kramnik match, he does not refer to it as a world championship match, but as a match between #5 and #6, and so on. Let's apply the same idea. Suppose we are given several lists L_1, L_2, ..., L_m, and we secretly favor one of them, call it L (so L is one of the above). We need to choose a weight W, and then use this same weight to compute each of D(W,L_1), D(W,L_2),..., D(W,L_m). As an example, think of L_1 being a rating list showing Kasparov as #1, L_2 another rating list with Kasparov on top, L_3 a rating list with Topalov as #1, and L_4 a rating list with Anand as #1. Suppose I want to choose a weight W which will make Topalov look good. So in this example m=4 and L=L_3. Returning to the general case, we are now ready to define the Cauchy-Danailov weights. Let L=(x_1,...,x_n) be our secretly preferred list, and denote as usual a_1=x_1-x_2, a_2=x_2-x_3,... Next, for each positive real number t, we define a Cauchy-Danailov weight W by letting: W=(ta_1,ta_2,...,ta_(n-1)).
In other words, W and the sequence of differences (a_1,...,a_(n-1)) are proportional. This follows Danailov's idea, in the sense that those differences among a_1,...,a_(n-1) which are large receive large weights, and those difference which are small receive correspondingly small weights. Sometime, by accident, this weight W may also help other lists among L_1, L_2,...,L_m. Usually it doesn't. But it always helps our secret list L, and that's the whole point of the Cauchy-Danailov weights. Why is Cauchy mentioned in this context? Because Cauchy's inequality accurately describes the effect of this type of weights. For any list L=(x_1,...,x_n), and the corresponding differences a_1,...,a_(n-1), and for any weight W=(w_1,...,w_(n-1)), Cauchy's inequality states that D(W,L)=w_1a_1+...+w_(n-1)a_(n-1) is less than or equal to (w_1^2+...+w_(n-1)^2)^(1/2)(a_1^2+...+a_(n-1)^2)^-
(1/2).
Moreover, we have equality here if and only if W and (a_1,...,a_(n-1)) are proportional, so if and only if W is a Cauchy-Danailov weight associated to L. In short: D(W,L) is a scalar product, which is maximized exactly by the Cauchy-Danailov weights. |
|
| Oct-19-09 | | Alexandru Z: The geometric interpretation of what was discussed in my previous post is as follows. A list L=(x_1,...,x_n) produces an (n-1) dimensional vector V=(a_1,...,a_(n-1)). Then, once we selected a weight W, the quantity D(W,L) is just the scalar product of the vectors W and V. Next, there is a notion of angle between any two vectors V and W, which is consistent with Cauchy's inequality. More precisely, if we denote this angle by theta, and denote the Euclidean norms (lengths) of V and W by ||V|| and ||W||, then the scalar product is given by: D(W,L)=||W|| ||V|| cos(theta).
Cauchy's inequality states that the scalar product in absolute value is less than or equal to ||W|| times ||V||. This is consistent with the equality above since cos(theta) in absolute value is at most 1. Moreover, cos(theta)=1 exactly when theta=0, so exactly when the vectors W and V have the same direction (are proportional). Now if we have several lists L_1,...,L_m and a fixed W, then D(W,L_1)=||W|| ||V_1|| cos(theta_1), and similarly for the others. Here the length ||W|| will appear in all of D(W,L_1),...,D(W,L_m), so it won't make a difference on the question of which of these numbers is the largest. Also, the lengths ||V_1||,...||V_m|| , which are not equal to each other, are anyway fixed, so there is nothing we can do about them, they are given to us from the beginning. So the only freedom we have is to play with the angles theta_1,...,theta_m. And what the Cauchy-Danailov weight W does is it arranges the preferred angle theta to be zero, in order to maximize the preferred scalar product D(W,L), and consequently to make the player on top of that list L look good. |
|
| Oct-20-09 | | Alexandru Z: As a concrete example, let us have a look at Topalov and Anand on <alexmagnus> dominator list: 7-8.Anand 95 Jul 98
9.Topalov 84 Jul 06
Let's see if we can help Topalov move in front of Anand by changing the weight as discussed above. First, we copy the July 2006 list, from #1 Topalov 2813 to #10 Gelfand 2729: L=(2813, 2779, 2761, 2743, 2742, 2738, 2734, 2732, 2731, 2729). Taking differences between consecutive elements in the list, we find: V=(34, 18, 18, 1, 4, 4, 2, 1, 2).
Let us compute the Euclidean norm of V. Its square is given by: ||V||^2=1156+324+324+1+16+16+4+1+4=1846.
Next, consider the July 1998 list. Anand is #2, and we help him a bit by considering the difference between #2 and #11, which is 105, instead of the difference between #2 and #10, which is 95 as computed by <alexmagnus>. We copy the list: L_1=(2795, 2780, 2730, 2725, 2720, 2720, 2715, 2710, 2700, 2690). Taking differences between consecutive elements, we obtain: V_1=(15, 50, 5, 5, 0, 5, 5, 10, 10).
The square of its Euclidean norm is:
||V_1||^2=225+2500+25+25+0+25+25+100+100=3025.
Not surprisingly, the length of V_1 is larger than the length of V. Also, we know from <alexmagnus> dominator list that if we define U=(1,1,1,1,1,1,1,1,1), then U has a larger scalar product with V_1 than with V. More precisely, the scalar product of V with U equals 34+18+18+1+4+4+2+1+2 = 84,
while the scalar product of U with V_1 equals
15+50+5+5+0+5+5+10+10 = 105.
But, if we take a vector W proportional to V,
W=tV=(34t, 18t, 18t, t, 4t, 4t, 2t, t, 2t), where t is an arbitrary positive real number, then the scalar product of W with V_1 will be smaller than with V. In other words, D(W,L) > D(W,L_1), and hence Topalov moves in front of Anand if we use the Cauchy-Danailov weight W. Indeed, D(W,L) = t||V||^2 = 1846 t,
while
D(W,L_1)= t(510+900+90+5+0+20+10+10+20)=1565 t. |
|
| Oct-21-09 | | Alexandru Z: <exponential weights> In connection with the data obtained by computing the difference between #1 and #10 on a given set of lists, some people may consider appropriate to also add the differences #10-#11, #11-#12, and so on, with smaller and smaller weights. One alternative would be to proceed as follows. Fix a real number t between 0 and 1, and consider the infinite sequence W=(1,t,t^2,t^3,t^4,...). Given a list L=(x_1,...,x_n), we define as usual a_1=x_1-x_2, ... , a_(n-1)=x_(n-1)-x_n. Then we extend this finite sequence to an infinite sequence by letting a_n, a_(n+1), ... be all equal to zero. Then define D(W,L) by D(W,L)=a_1+a_2t+a_3t^2+a_4t^3+...
Note that if t=0, D(W,L) reduces to the difference between #1 and #2 on the list L. If t=1, D(W,L) equals the difference between #1 and the last element of the list L. For 0<t<1, D(W,L) takes values between the above two extreme cases. A nice feature of these weights W, which other weights do not possess, is that if we remove x_1 from the list L, and denote the resulting new list by L*, then: D(W,L) = a_1 + t D(W,L*).
Recall our interpretation of D(W,L) as a measure of how much x_1 dominates the rest of the list L, with respect to the weight W. Then the above simple formula establishes a connection between how much x_1 dominates the rest of the list L, and how much x_2 dominates the remaining elements, with respect to the <same> weight W. Also, a_1 is just the rating difference x_1-x_2. For example, if we look again at the July 1998 list, the above formula provides a relationship between how much #1 Kasparov dominates the other players and how much #2 Anand dominates the rest of the list after removing Kasparov, as a function of t and the rating difference between Kasparov and Anand. As a side comment, there are many sequences of interest in number theory, and it would be interesting to study some of them from this dominator perspective introduced by <alexmagnus>. As a simple example, how much would we say the number zero dominates the negative numbers? With respect to the above weights, the answer is nice and simple: L=(0,-1,-2,-3,...), a_1=1, a_2=1,...
D(W,L) = 1+t+t^2+... = 1/(1-t).
As a variation of the above question, let's say every third number starting with -1 loses a rating point. So -1, -4, -7,... become -2,-5, -8, ... Then the domination of 0 will be slightly stronger than before. Again we can compute D(W,L) in closed form, as a rational function of t. L=(0,-2,-2,-3,-5,-5,-6,...). The sequence of differences is (2,0,1,2,0,1,...), and D(W,L) = 2+t^2+2t^3+t^5+2t^6+t^8+...
= 2(1+t^3+t^6+...)+t^2(1+t^3+t^6+...)
= (2+t^2)/(1-t^3). |
|
| Oct-21-09 | | Alexandru Z: <power weights>
The above weights W=(1,t,t^2,...) have w_m=t^(m-1), which for fixed t decays exponentially fast as m increases. If instead we want w_m to go to zero in a more moderate way, like a power of m say, then we can fix a positive real number s and let w_m=1/m^s. Then W=(1, 1/2^s, 1/3^s, 1/4^s, 1/5^s,...),
and for a given list L=(x_1,...) producing the sequence of differences a_1, a_2,...
we have
D(W,L)= a_1+a_2/2^s+a_3/3^s+...
If L is a finite list, the case s=0 corresponds to the difference between x_1 and the last element of L, while if we let s go to infinity then D(W,L) approaches the difference x_1-x_2. These were also the two extreme cases in the previous post. The difference is that in the previous post D(W,L) was a power series in t (respectively a polynomial if the list L was finite), and now it is a Dirichlet series. Power series and Dirichet series behave quite differently. For example, in the problem of how much zero dominates the negative numbers, working with these new weights gives: L=(0,-1,-2,...). Differences: 1,1,1,...
D(W,L) = 1+1/2^s+1/3^s+1/4^s+... = zeta(s),
the Riemann zeta function computed at s. This holds for s > 1. Zeta(s) has analytic continuation to the entire complex plane, except at s = 1 where it has a pole, and satisfies a functional equation relating zeta(s) to zeta(1-s). To wrap up this entire discussion, let's also have a look at that variation where each of the numbers -1, -4, -7, ... looses a rating point. L=(0,-2,-2,-3,-5,-5,-6,...). Differences: 2,0,1,2,0,1,... Now the idea is to write this sequence of differences as a sum of two sequences: 1,1,1,1,1,1,... and 1,-1,0,1,-1,0,...and realize that this last sequence corresponds to the unique non-principal Dirichlet character modulo 3, call it chi. Therefore: D(W,L) = zeta(s) + L(s,chi).
Diriclet L-functions L(s,chi) associated to non-principal characters don't have poles. They too satisfy functional equations, which are similar to the functional equation satisfied by the Riemann zeta function, but also involve other arithmetical quantities such as Gauss sums. |
|
Oct-31-09
 | | alexmagnus: Hm, the November list is up. Th rating of #10 is 2748. That makes two playrs having domination scor over 50 (i.. enough for my list). Topalov has 62, whch is below his peak (84). Carlsen's 53 is his peak (previously he was off the list). So, the new domination list looks like this: Kasparov 175 Jan 90
Fischer 160 Jul 72
Karpov 130 Jan 89
Ivanchuk 105 Jul 91
Kramnik 102 Okt 02
Tal 100 Jan 80
Korchnoi 95 Jan 79
Anand 95 Jul 98
Topalov 84 Jul 06
Spassky 80 Jan 69
Shirov 65 Jul 94
Gelfand 60 Jan 91
Kamsky 60 Jan 96 Jul 96
Morozevich 56 Jul 99
Jussupow 55 Jul 86
Timman 55 Jan 90
Adams 53 Jul 00
Carlsen 53 Nov 09
Botvinnik 50 Jan 69
Portisch 50 Jan 80
Bareev 50 Jul 91 |
|
Oct-31-09
 | | alexmagnus: Another observation is the rating of #20. It fell again and is 2719 now. |
|
Oct-31-09
 | | alexmagnus: The average birthyear of the top-10 is 1978.8, for average age of 31. |
|
Oct-31-09
 | | alexmagnus: Browsing through games of my first opponent ever, I stubled upon this one: Zs. Szajbély - P. Baki (2161)
1. e4 e5 2. Nf3 d6 3. d4 Nd7 4. Bc4 c6 5. dxe5 dxe5 6. Ng5 Nh6 7. O-O Be7 8. Ne6 fxe6 9. Bxh6 Nb6 10. Qh5+ Kf8 11. f4 Qd4+ 12. Kh1 Bf6 13. fxe5 gxh6 14. Rxf6+ Ke7 15. Rf7+ 1-0 Crazy. At least somebody lost to him quicker than I did, and that soebody would himself beat me in 15 moves ;). But hell, I never saw bad opening being punished like this. |
|
Oct-31-09
 | | alexmagnus: [Event "Wertungspartie, 5m + 0s"]
[Site "Großer Spielsaal"]
[Date "2009.11.01"]
[Round "?"]
[White "Enerji"]
[Black "Kampfgeist"]
[Result "0-1"]
[WhiteElo "1323"]
[BlackElo "1371"]
[PlyCount "30"]
[EventDate "2009.11.01"]
[TimeControl "300"]
1. e4 e5 2. Nf3 Nc6 3. Bc4 Nf6 4. Ng5 Bc5 5. Nxf7 Bxf2+ 6. Kf1 Qe7 7. Nxh8 d5 8. exd5 Bg4 9. Be2 Bxe2+ 10. Qxe2 Nd4 11. Qxf2 O-O-O 12. Na3
Rf8 13. Kg1 Ne4 14. Qe1 Qc5 15. Qxe4 Ne2# 0-1 |
|
Oct-31-09
 | | alexmagnus: Another comparison from a different sport showing that human brain on top level does progress and therefore it is possible there is no inflation: memory sport. The norm for a memory grandmaster got higher and higher with the time... Note, memorizing is absolute, unlike rating numbers, is absolute. Still we have kind of "inflation" here if we'd assumed them being not absolute ;) |
|
Oct-31-09
 | | alexmagnus: The first world championship in memorizing was organized in 1991. All records are from 2003 or later, all but two from 2005 or later: http://web.aanet.com.au/memorysport... |
|
Oct-31-09
 | | alexmagnus: But what's good is that in memory sports you <can> compare "players" over time. Here is the overall world ranking (as you see, best result is the ranking - it is also shown where and when it was achieved: http://web.aanet.com.au/memorysport... The domination of new "players" is obvious. |
|
Oct-31-09
 | | alexmagnus: In 1993, the world memory champion actually would miss today's GM norm in two of 3 disciplines counted for the title (and in the one he'd make it, it would be exactly the norm). |
|
 |
 |
|
< Earlier Kibitzing · PAGE 22 OF 57 ·
Later Kibitzing> |
|
|
|




![]()
![]()

